Inductive Graph Embeddings through Locality Encodings

General
,
1

Authors:

  • Nurudin Alvarez-Gonzalez
  • Andreas Kaltenbrunner
  • Vicenç Gómez

tl;dr

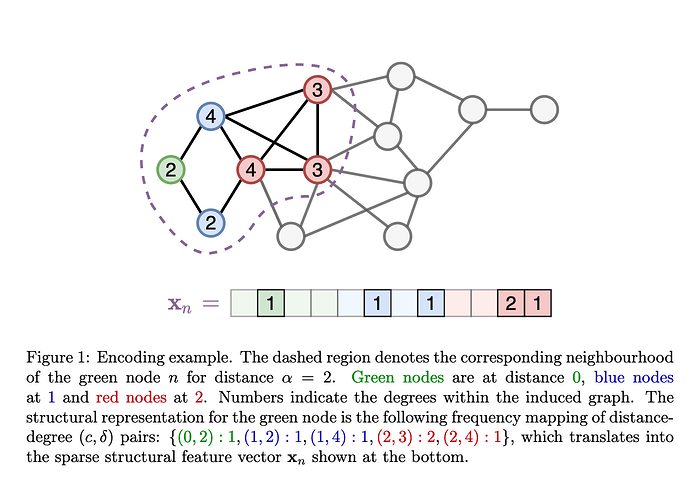
Creates features of a node by encoding the degree and distance of the nodes in the neighborhood. Neighborhood size is a hyperparameter, \alpha. The size of the resulting vector is \alpha \cdot d_\text{max}. The values of this (sparse) vector are the count of the number of nodes that satisfy that degree/distance criteria.

This local encoding is then simply passed through a linear layer to densify and embed.

Encoding example
Encoding example1380×966 118 KB

Experimental Setting

Datasets

  • Les Miserables
  • Sister Cities
  • Facebook
  • ArXiv AstroPhysics
  • PPI

Baselines

  • Unattributed graph embeddings (all transductive):
    • DeepWalk
    • node2vec
    • LINE (Line: Large-scale information network embedding)
    • VERSE (Verse: Versatile graph embeddings from similarity measures)
  • Inductive methods (all require node attributes):
    • GCN
    • GraphSAGE
    • LGCL (large-scale learnable graph convolutional networks)
    • PinSAGE

Evaluation metrics

Unsupervised

Samples random walks from each node. Then use a skip-gram negative sampling objective.

Run this to generate embeddings and then cluster on the embeddings. In Les Miserables (which have two copies of the graph with a single edge between a random pairing across graphs), they find that by setting the receptive field of the structure encoding to \alpha=1, clusters mostly capture densely connected nodes. However, when \alpha=2, cluster assignment is more based on structural role and less so on node proximity.

Also look at ROC-AUC on Link Prediction tasks using Facebook and ArXiv datasets.

Supervised

Exactly what you’d expect–use these as input embeddings to a downstream model.

Multi-label node classification task where the objective is to predict 121 different binary labels capturing protein functions in a series of Protein-to-Protein Interaction (PPI) graphs.